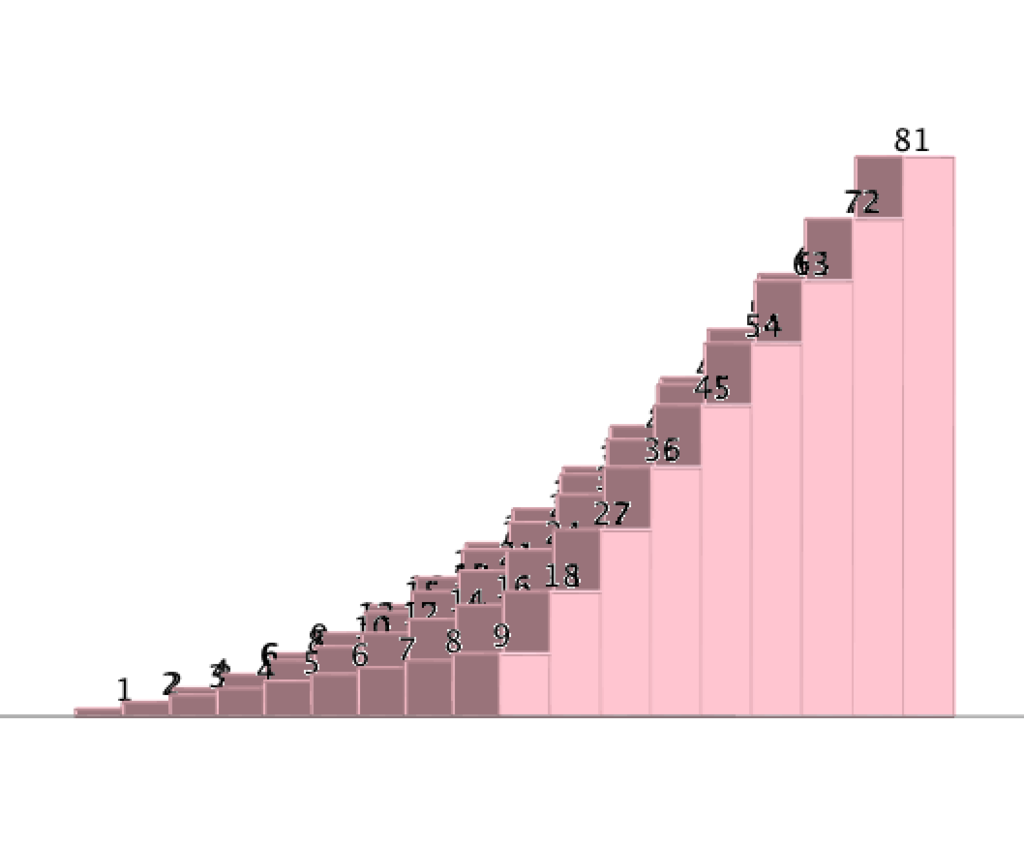
九九の視覚化、流行ってますね。発端はこちらです。
昔、自分が欲しかった表を作りました。
— まうどん🔵4/2〜8は発達障害啓発週間 (@mauzoun) 2017年3月29日
ふつうの九九表の、補助教材として使えるかも… pic.twitter.com/x19P5utcNr

引用元:twitter(@mauzoun)
なるほど。数が増えていく感がわかりやすいですね。これをきっかけにして全国的に九九の視覚化ブームが発生し、次のようなものも現れました。
@mauzoun 非常に面白いし良いと思います。ただ、個人的には順序が変わると面積が変わってしまい、交換法則が逆に理解しづらくなるぶん改良の余地ありと感じました。私案貼っときますのでご参考まで。 pic.twitter.com/w6bqVaacmk
— Yutaka tanida (@L_star) 2017年3月30日
九九のビジュアル理解ってこうとちゃうの? pic.twitter.com/UNYcV0gJfs
— 職人/げるびらりあ (@gervillaria) 2017年3月31日

引用元:twitter(@L_star)

引用元:twitter(@gervillaria)
おお! こっちは数が増えていくことも、2つの数をかけたら面積だということも、×の前後を交換しても積が変わらないこともわかってとてもいい図ですね!
さて、この流れが面白かったので流行りに乗って私も九九を可視化してみました。こちらです。
九九を視覚化するやつhttps://t.co/vH15FwMnfe pic.twitter.com/6rccB4mVeZ
— 鯵坂もっちょ (@motcho_tw) 2017年4月3日
九九立体の構造
なかなか面白い図になりました。画像単体で見てみます。

つまり、行の数と列の数の積を高さで表現してあるわけですね。回してみましょう。

今回はこの立体を使ってめちゃくちゃ遊びます。
便宜的にこいつのことを「九九立体」とでも呼びましょう。九九立体をじっと見てると、いろいろなことに気づきます。まずこう、何ていうんですかね。絶妙なヘコミ感みたいなものが見て取れますね。
そもそもこの九九立体、それぞれの数字が書いてある部分、つまり角柱の上面部は、という曲面の上に乗っています。

の曲面
このという式は、縦の値(
)と横の値(
)をかけると高さの値(
)になる、という構造を表しています。これはつまり九九立体の構造そのものです。この曲面がもつヘコミ感こそが、九九立体のヘコミ感の正体だったというわけです。

確かに上面の正方形の頂点の一つが、曲面の上に乗っていることがご確認いただけるかと思います。
平方数について
いんいちがいち、ににんがし、さざんがきゅう……という同じ数どうしをかけた数の列は、すなわちの
に自然数を入れた数の列になります。平方数ですね。

九九の中の平方数
というわけでこの立体をナナメから見てみると……。
ちゃんとが描く放物線が見える!!
この立体は見た目のわかりやすさのために実際の高さよりも低くして、つまり上からギュッと押しつぶしてあります。そのため、実際に見えているのはくらいの感じの放物線となってます。
押しつぶさず、そのままの高さで表現してみた九九立体がこちらです。

これはこれでエンパイアステートみたいでかっこいいですね! 隣の段との差もこっちのほうがわかりやすいです。下の方は数が詰まっているのに上の方はスカスカなんだなぁ〜ということが見て取れます。
同じ数をつないでみる
今度はこの九九立体の段数を増やしてみます。

20×20までにしてみました。こんなもん暗記させられなくてよかったですね。
この立体も眺めていると、ここに「現れない数」もあれば「たくさん現れる数」もあるということに気づきます。たとえばたくさん現れる24は4×6、6×4、3×8、8×3、2×12、12×2の6箇所に出現します。さて、ではこの6箇所を繋ぐとどういう形が現れるでしょうか?
それを知るために、九九立体を水浸しにします。

水位24で水浸しにしてみました。なんらかの曲線が現れましたね! 水位を120くらいまであげてみます。

やはり曲線が見えます。今度は動画で。

九九の表において、同じ数をつなげたときに現れるこの曲線はつまり「(
は定数)」を満たす点の集合です。「
」の形に式変形するとこの式は
となり、要するに双曲線だったわけです。九九の表で同じ数をつなげると双曲線が現れる、と。
一般化する
今度はじゃあこの九九を一般化するとどうなるでしょうか? 「一般化」と言ってもいろいろな方向性がありえますが、じゃあ一体どう一般化するのか? こうですよね。

そうだね。九九九だね。自分で作っといてなんですがこんなもんいつまででも見続けられてしまいます。
こちらに関してもいろいろ見えてきます。特に、中心部にある25、50、75、100...っていう25の段の柱が不動点としてずっと見えてるのが面白いですね。あとなんとなく双曲面も見える気がします。ほかにも面白い発見があったらこっそり教えてください。
こうなってくると次に見てみたいのは当然九九九九、さらに九九九九九とかになってくるわけですが、これらを表現するのは3次元である九九九ほど簡単ではありません。しかしやりようはいくらでもあって、例えば時間経過で数を変化させるとか、色を変えて表現するとか、あらかじめ4次元を見えるようにしておくなどの方法が考えられます。こちらもいい表現ができましたら是非教えてください。
九九に現れない数
先ほどの考察で「九九にたくさん現れる数」を考えると双曲線がでてくることがわかりましたが、では今度は「九九に現れない数」を考えるとどうなるでしょうか?
結論から申し上げますと、この問いは魔界です。どうしても考えてみたいという方は以下のトゥギャッターをご参照ください。
おわりに
九九の視覚化を考えていたら、かなり高度な数学までたどり着いてしまいました。
先日、数学がめっちゃできる中高生の方々とお話しさせて頂く機会があったのですが、やっぱりそういう方って学校の授業とかつまんないのかな?と思って聞いたら「いや、学校で習うことも一般化したり、発展させたりすれば高度な数学につながっていることが多いので楽しい」とおっしゃっていました。今回の話はまさにそういう話だったのではないかなと思います。
小学校で習うからこそ、簡単だと思われている「九九」。そんな簡単な概念にすら、こんなに奥深い数学が潜んでいたということです。「にすら」とか言ってしまいましたが、それはとりもなおさず「簡単さ」「初等的かどうか」「とっつきやすい概念かどうか」は数学の面白さとは無関係ということを意味します。
数学を楽しむのに、高度な数学を知っている必要は必ずしもないと思います。この記事において、九九のような身近な概念を使って数学の楽しさに触れることができた、ということがその証左といえるのではないでしょうか。
ではまた!